結婚しました
ご質問があればこちら
続きを読むこの記事では Open Telemetry のトレースの機能を使います。トレースを使うと、サーバーを越境してコールグラフとその実行時間などを取得することができます。下の画像は Jaeger のスクリーンショットです。Jaeger は Open Telemetry の規格にのっとったコレクター実装のひとつです。
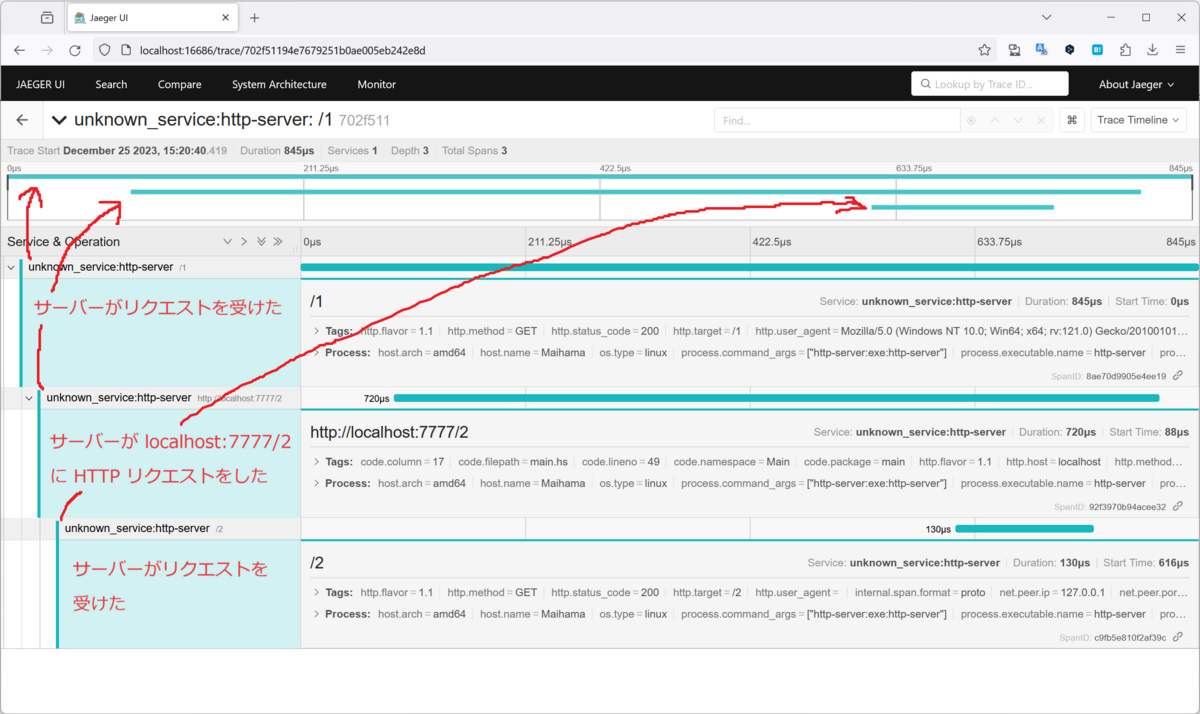
この例では HTTP サーバーと HTTP クライアントでトレースを取得しています。まずサーバーが /1 のパスでリクエストを受けつけたことが分かります。このリクエストに対してレスポンスを返すまでに 845μs かかっていますね。このトレースにおけるひとつの区間をスパンといいます。
次にサーバーはこのリクエストに対して処理をする途中で localhost:7777/2 に HTTP リクエストを投げたことが分かります。リクエストを投げてレスポンスが返ってくるまでに 729μs かかっています。
最後に /2 へのリクエストに対してサーバーが応答したスパンが記録されています。
この例では便宜上、サーバーは自分に対して再度リクエストをしていますが、これは物理的なサーバーが別であっても同様にトレースが取得できます。
Open Telemetry はプログラミング言語や OS などに依存しない仕様ですから、Haskell でもトレースを記録したいです。そうすれば Istio や Node などのスパンとつながったトレースを見ることができます。Haskell では hs-opentelemetry ライブラリーを使用します。
自分もいっぱいコントリビュートしています。HERP 社からの委託を受け開発しています。
インターフェースは今後破壊的変更が入る可能性が多分にありますが、HERP 社で本番運用している程度に完成しています。
hs-opentelemetry はいくつかのパッケージに分かれています。まず基本となるものは hs-opentelemetry-api と hs-opentelemetry-sdk です。api と sdk に分かれているのは Open Telemetry の仕様が分けるよう指示しているためであまり意味はありません。トレースを取得するためのトレーサーおよびトレーサーを作成するためのトレーサープロバイダーを作成するために使用します。また「ここからここまでスパンを取得する」というように手動で指定する場合に使用します。手動で指定するには下記の型をもつ inSpan 関数を使用します。
module OpenTelemetry.Trace.Core … inSpan :: (MonadUnliftIO m, HasCallStack) => Tracer -> -- | The name of the span. This may be updated later via 'updateName' Text -> -- | Additional options for creating the span, such as 'SpanKind', -- span links, starting attributes, etc. SpanArguments -> -- | The action to perform. 'inSpan' will record the time spent on the -- action without forcing strict evaluation of the result. Any uncaught -- exceptions will be recorded and rethrown. m a -> m a
inSpan の第4引数の所要時間をスパンとして記録します。
これでスパンは記録できますが、全部を inSpan で書いていくのはいささか邪魔くさいです。そこでインスツルメンテーションが用意されています。初めのトレースの例では wai 用のインスツルメンテーションと http-client インスツルメンテーションを使用しています。インスツルメンテーションを使用すると初めのトレースの例の実装は下のようになります。
{-# LANGUAGE OverloadedStrings #-} import qualified Network.HTTP.Client as H import qualified Network.HTTP.Types.Status as H import qualified Network.Wai as W import qualified Network.Wai.Handler.Warp as W -- Network.HTTP.Client の代わりに he-opentelemetry のインスツルメンテーションを使用する import OpenTelemetry.Instrumentation.HttpClient ( Manager (), defaultManagerSettings, httpLbs, newManager, ) -- he-opentelemetry のインスツルメンテーションで提供される WAI ミドルウェアを使用する import OpenTelemetry.Instrumentation.Wai (newOpenTelemetryWaiMiddleware) import OpenTelemetry.Trace ( initializeTracerProvider, setGlobalTracerProvider, ) main :: IO () main = do -- デフォルト設定でトレーサープロバイダーを作成する tracerProvider <- initializeTracerProvider -- グローバルな IORef に作成したトレーサープロバイダーを参照させる setGlobalTracerProvider tracerProvider -- トレースが取れるようラップされた http-client を作成する httpClient <- newManager defaultManagerSettings -- トレースを取得する WAI ミドルウェアを作成する tracerMiddleware <- newOpenTelemetryWaiMiddleware W.run 7777 $ tracerMiddleware $ app httpClient app :: Manager -> W.Application app httpManager req res = case W.pathInfo req of ["1"] -> do newReq <- H.parseRequest "http://localhost:7777/2" newRes <- httpLbs newReq httpManager res $ W.responseLBS H.ok200 [] $ "1 (" <> H.responseBody newRes <> ")" ["2"] -> res $ W.responseLBS H.ok200 [] "2" _ -> res $ W.responseLBS H.ok200 [] "other"
app 関数はこれまで通りの書きごこちですが、HTTP リクエストを受けてレスポンスを返すまで、HTTP リクエストを投げてレスポンスを受けるまでのスパンが取得できるようになっています。簡単ですね。
インスツルメンテーションには他にも mysql-simple 版や grpc-haskell 版などが用意されています(というか作成しました)。また Datadog 仕様のトレースと接続するためにプロパゲーターなども用意されています(これも作成しました)。
実際に手元で動かしてみたい場合はリポジトリーの examples ディレクトリーを参照してください。
Open Telemetry を活用してオブザーバビリティーを上げていきましょう。
それではメリークリスマス!
これは Haskell アドベントカレンダー 2023 25日目の記事です。

カトーのタキ1000 1000号入りセットを買ったので、アーノルトカプラーをグリーンマックスのナックルカプラーに換えた
すると、機関車との高低差が大きく登坂後に解結してしまった
この連結部高低差、わが家のレイアウトで解結する…… pic.twitter.com/KWrpvIci00
— 💭 技術書典 14 お03 5月21日 (@kakkun61) 2023年5月3日
そんなわけでカプラー(連結器)を作った
カプラーです pic.twitter.com/wQVXh0LMQT
— 💭 技術書典 14 お03 5月21日 (@kakkun61) 2023年5月3日
これを3度ぐらい現物合わせで修正していい感じになったらディテールを追加する
ディテールを足した pic.twitter.com/K5avDDp7ax
— 💭 技術書典 14 お03 5月21日 (@kakkun61) 2023年5月7日
パラメーターの問題なのかうちの造形機の問題なのか分からないけどディテールうまく出なかった
制作過程らしき動画
作る過程見れるやつ pic.twitter.com/vVy2Ymb45q
— 💭 技術書典 14 お03 5月21日 (@kakkun61) 2023年5月7日
STL は CC BY 4.0 で公開するので許可された範囲で好きに使ってほしい
現状の dot ファイルのたぐいをメモするついでに人に見せる形でまとめておこうと思う。
自分の思想として「フレームワークよりライブラリー」というのがあるので、プロシージャーの形で定型処理をまとめておいて実際の dot ファイルはプロシージャーを呼び出すようにしている。
Linux ではデフォルトのことが多い Bash を使っている。
リポジトリーをクローンしてきたところに各種 example を置いてあるので、それをコピーしてきて随時そのマシンに合わせて書き換える。
cd mv .profile .profile.back mv .bashrc .bashrc.back mv .bash_logout .bash_logout.back dot_files='path/to/this/repo' cp "$dot_files/bash/.bash_profile.example" .bash_profile cp "$dot_files/bash/.bashrc.example" .bashrc cp "$dot_files/bash/.bash_logout.example" .bash_logout # edit .bash_profile .bashrc .bash_logout
.bash_profile はこんな感じ。
# dotfiles リポジトリーのディレクトリーを指定する dot_files=. # ここでプロシージャーを定義してあるライブラリーをロードする # shellcheck source=/dev/null source "$dot_files/sh/lib.sh" # shellcheck source=/dev/null source "$dot_files/bash/lib.bash" # ~/.bin とかを PATH に追加 add_local_bin # shellcheck source=/dev/null source "$HOME/.bashrc" # X 環境なら setup_sands # SSH エージェントを起動 # WSL2 の場合は Windows で起動してあるエージェントにつなぎに行くようにしてある(が、ちょっとバグってる # くわしくは https://kakkun61.hatenablog.com/entry/2022/06/28/WSL2_%E3%81%AE_SSH_Agent_%E7%9B%86%E6%A0%BD start_ssh_agent # start_ssh_agent_wsl # もろもろ設定のための環境変数の定義 setup_gpg setup_git_env setup_saml2aws
.bash_logout は SSH エージェントの後始末だけ。
.bashrc はこんな感じ。
# この辺は .bash_profile と一緒 dot_files=. # shellcheck source=/dev/null source "$dot_files/sh/lib.sh" # shellcheck source=/dev/null source "$dot_files/bash/lib.bash" # もろもろ設定 # 環境変数の定義したり eval したり source したり setup_nix setup_less setup_prompt "$dot_files" setup_dircolors setup_bashmarks "$dot_files" setup_fuck setup_bash_config setup_ls setup_shellcheck setup_direnv setup_git_completion "$dot_files"
あんまり多くは使ってないが使ってるのは次のような感じ。
fuck と打てばよくなるしごとでないときは Windows で PowerShell を使っている。
PowerShell には標準でパッケージマネージャーが付いてくるので外部ライブラリーを入れるのが簡単。
[Diagnostics.CodeAnalysis.SuppressMessageAttribute('PSAvoidUsingInvokeExpression', '', Justification = 'For the fuck')] param () # dotfiles リポジトリーのディレクトリーを指定する $dotFiles = '.' # 自前ライブラリーをインポート . $dotFiles\pwsh\lib.ps1 # 外部ライブラリーをインポート Import-Module Posh-Git Import-Module posh-sshell Import-Module PSBookmark Import-Module psake Import-Module ghcman Import-Module path-switcher Import-Module code-page Import-DotenvModule # SSH エージェントの起動 Start-SshAgent -Quiet # 環境変数の設定とかローカルの ps1 ファイルのインポートとか Initialize-Chocolatey Initialize-Python # the fuck Invoke-Expression "$(thefuck --alias)" # prompt Set-Item -Path Function:\prompt -Value (Get-Prompt) -Options ReadOnly # arduino . $dotFiles\lib\arduino-cli\completion.ps1
この年末年始に NixOS 機が1つできたのでそれは当然 /etc/nixos/configuration.nix で管理しているが、home-manager までは手が出ていない。
RSS 監視して Discord に投げるやつ Raspberry Pi で動かすか
— を゙ (@kakkun61) 2022年7月24日
これをしようとコードを書いた。クロスコンパイルの容易さから Go で書いた。Raspberry Pi 2 Model B で動かしている。
ひとつめは feed-trigger。
これは RSS をチェックして更新があると指定されたコマンドの標準入力に新規エントリーのみを含めたフィードを渡して起動するやつ。
ふたつめは discord-feed-post
これは標準入力から取得した RSS フィードを Discord に投稿するやつ。
これらふたつを合わせて cron で1時間に1回起動するようにした。
これがしたかった。
hoge path/to/dir foo bar って実行したら、ワーキングディレクトリーが path/to/dir で foo bar コマンドを実行してくれるような hoge コマンドない?
— かずき (@kakkun61) 2022年8月11日
$ wd ディレクトリー コマンド オプション
とすると「ディレクトリー」をワーキングディレクトリーにして「コマンド」を「オプション」付きで実行する。
pushd でもできるけど popd と合わせるとタイプ数が多かった。
GitHub のリリースページに Windows・Linux・macOS (x64) 用のバイナリーがある1。
自分でビルドする場合は cabal と ghc が必要。
$ make install
気に入ったら GitHub にスターをよろしくね。